|
Basics of Positional Astronomy and Ephemerides
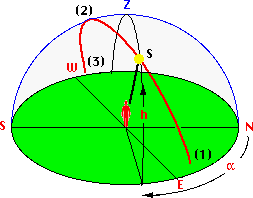
The observer is located at the centre of his "celestial sphere" with zenith Z above his head and the horizon N-E-S-W. The Sun, Moon or any other celestial body can be identified by the two coordinates altitude h and azimuth alpha (horizontal coordinates). Altitude is the angular distance above the horizon: 0 <= h <= 90°, and azimuth is the angular distance, measured along the horizon, eastward from the North point N (as in nautics): 0 <= alpha <360°. The daily movement of an object - resulting
from the rotation of the Earth on its axis - starts
when it rises
at (1). At (2) it passes across the observer's meridian
NZS (transit), and it sets
at (3). Details about the difference
between transit and culmination Please watch the Java applet Apparent Movement of a Star (on this server, with kind permission of Walter Fendt). The horizontal coordinates of an object depend on the location of the observer on the Earth (and on time). In astronomy equatorial coordinates are commonly used when giving the position of an object on the celestial sphere. The equatorial system is based on the celestial equator, which is the great circle obtained by projecting the Earth's equator on to the celestial sphere, the equatorial plane being perpendicular to the Earth's axis of rotation. 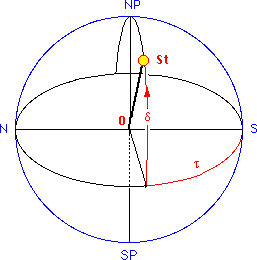
The first equatorial coordinate is declination
delta, measured in degrees north and south of the
celestial equator (N: 0° < delta < 90°, S: 0°
> delta > - 90°. The second coordinate, may be
the hour angle
tau, measured along the equator from the meridian
S-NP-N of the observer to the hour circle
SP-St-NP of the star St. The hour angle corresponds to
the length of sidereal time elapsed since the body St
last made a transit of the meridian.
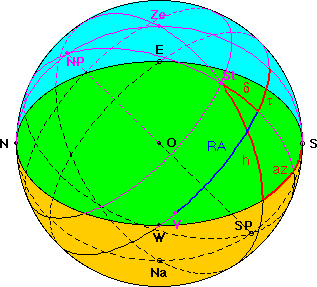 To convert equatorial coordinates hour angle and declination (tau, delta) to horizontal coordinates azimuth and altitude (az, h), the "nautical triangle" NP-Ze-St is used: NP-St = 90° - delta, Ze-St = 90° - h. From spherical trigonometry we get: tan az = (- sin tau) / (cos beta tan delta - sin beta cos tau) Example: The second equatorial coordinate may also be
right ascension
RA, measured in hours, minutes and seconds of time,
taking into account the rotation of the celestial
sphere once in 24 hours of sidereal time. The zero
point for right ascension is taken as the northern vernal equinox. Right ascension RA, hour angle tau and sidereal time theta are related by: tau = theta - RA Animation: |
1.
Conversion of date and time: local time to universal time UT 15 h CEST = 13 h UT convert time: Julian Day of 1991/ 5/19 at 13 UT Julian day of 2000/01/01 at 12 UT
number of Julian days since 2000/01/01
at 12 UT number of Julian centuries since
2000/01/01 at 12 UT JD = 2448396.04167 JD = 2451545.0 -3148.95833 2. Astronomical
algorithms: compute the ecliptic latitude B B = -1.87° convert ecliptic latitude and longitude to
right ascension RA and declination delta RA = 133.44° = 8.8962 h compute sidereal time (degrees) at
Greenwich local sidereal time at longitude 10° E
local hour angle theta0 = 71.698° theta = theta0 + 10° = 81.698° tau = theta - RA = 81.698° - 133.46° 3. Final results
convert (tau, delta) to horizon coordinates (h,
az) of the observer (50° N, 10° E) The function
atan2(numerator,denominator) should be used to
avoid ambiguity. true (geocentric) altitude: h = 36.1° azimuth angle: az = 110.6° from N p = 0.80°
The refraction R is calculated by
Saemundsson's formula (Meeus, Astronomical Algorithms): h is the true (airless) altitude in
degrees, R is in minutes of arc. The apparent
(measured) altitude is h+R. R = 0.0004° apparent altitude h h = 36.1° - 0.80° = 35.3°
compute the position of the Moon
on 1991/05/19 at 15:00 CEST
Berechnung der Mondposition
used by the algorithm for B and L
T = - 3148.95833/36525
= - 0.0862137805
and the longitude L
of the Moon
L = 131.52°
delta = 15.53°
= -51.74° = 308.25°
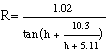
(corrected for parallax and
refraction)