Eccentricity of the orbit of the Earth from 1,000,000 BC to 1,000,000 AD

Eccentricity of the orbit of the Earth

from 1,000,000 BC to 1,000,000 AD

According to Meeus (More Mathematical Astronomy Morsels, Chapter 33) Bretagnon published in 1984 an algorithm for the eccentricity e valid for a very long period of time:

The time T is expressed in thousands of years from the epoch 1850.0. The sums have 19 terms.
This method gives good results from 1,000,000 BC to 1,000,000 AD.

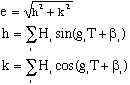
Compute the eccentricity by JavaScript:

Year (-1,000,000 .. 1,000,000):

Eccentricity e =

Write a table by JavaScript:

The Earth's orbital eccentricity changes with a period of about 100,000 years in the range of to 0.06:

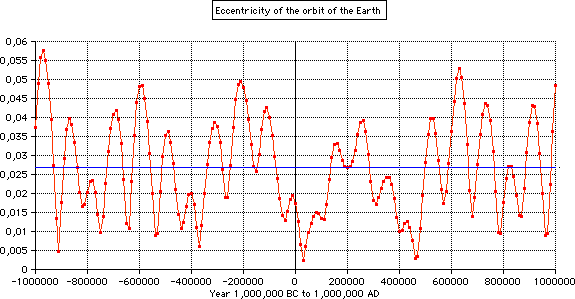
The mean value of the eccentricity is 0,02674, the present value is 0.01670.

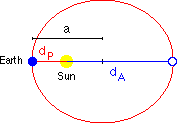
The perihelon distance d_P for an ellipse of semimajor axis a and eccentricity e is:
d_P = a*(1 - e)
d_P / a = 1 - e

The amount of solar radiation S received by the Earth ( "insolation") is proportional to the square of the inverse:
S ~ (a/d_P)²

Year Eccentricity e Perihelion distance
d_P/a = 1 - e S ~ a²/d_P² Ratio of radiation
S / S₂₀₀₀ Deviation
from 2000

2,000 0.01671 0,98329 1,03427 1 +/- 0 %

-970,000 0.05767 0,94233 1,06673 1,08883 + 9 %

30,000 0.00231 0,99769 1,00463 0,97134 - 3 %

Year Eccentricity e Aphelion distance
d_A/a = 1 + e a²/d_A² Ratio of radiation
S / S₂₀₀₀ Deviation
from 2000

2,000 0.01671 1.01671 0.96740 1 +/- 0 %

-970,000 0.05767 1.05767 0.89392 0.92404 - 8 %

30,000 0.00231 1.00231 0.99540 1.02894 + 3 %

Perihelion
For the minimum value of the eccentricity e the amount of solar radiation received by the Earth (insolation) is 3 % less than at present, and for the maximum value of e the radiation is 9 % greater than at present.
Aphelion
For the minimum value of the eccentricity e the amount of solar radiation received by the Earth (insolation) is 3 % greater than at present, and for the maximum value of e the radiation is 8 % less.
The difference of the insolation at perihelion and at aphelion is 7 % at present, and 17 % for the maximum eccentricity.

Variations for 4,000 BC to 8,000 AD

2006, Mar 24

Year	Eccentricity e	Perihelion distance d_P/a = 1 - e	S ~ a²/d_P²	Ratio of radiation S / S₂₀₀₀	Deviation from 2000
2,000	0.01671	0,98329	1,03427	1	+/- 0 %
-970,000	0.05767	0,94233	1,06673	1,08883	+ 9 %
30,000	0.00231	0,99769	1,00463	0,97134	- 3 %

Year	Eccentricity e	Aphelion distance d_A/a = 1 + e	a²/d_A²	Ratio of radiation S / S₂₀₀₀	Deviation from 2000
2,000	0.01671	1.01671	0.96740	1	+/- 0 %
-970,000	0.05767	1.05767	0.89392	0.92404	- 8 %
30,000	0.00231	1.00231	0.99540	1.02894	+ 3 %