|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Miscel- laneous |
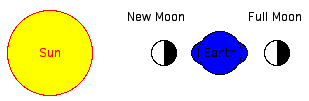 High tides at the sublunar point and its antipodal point at New Moon and Full Moon. The tidal forces of the Moon is reinforced by the Sun (spring tide): a ≈ aMoon + aSun ≈ (1.1 + 0.50)⋅10-6 m/s2 = 1.6⋅10-6 m/s2 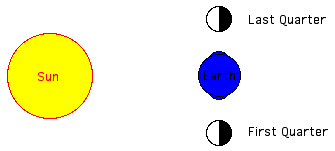 When the Moon is at first quarter or third quarter (Sun and Moon separated by 90° when viewed from the Earth) the solar tidal force partially cancels the Moon's (neap tide): a ≈ aMoon - aSun ≈ (1.1 - 0.50)⋅10-6 m/s2 = 0.60⋅10-6 m/s2 The axial tidal acceleration a by the Moon is approximately: 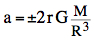 Earth's radius r=6371 km, Moon's mass M=7.349 1022 kg, mean distance Earth-Moon R =384401000 m: aMoon ≈ 1.1⋅10-6 m/s2 Sun's mass M=1.989 1030 kg, mean distance Sun-Earth R=1.496⋅1011 m aSun ≈ 0.50⋅10-6 m/s2 The applet is using the ecliptical
geocentric longitudes of the Moon and the Sun
(neglecting their declinations), and the
geocentric distances of the bodies.
Select "Draw Tides" from the "Details" menu: 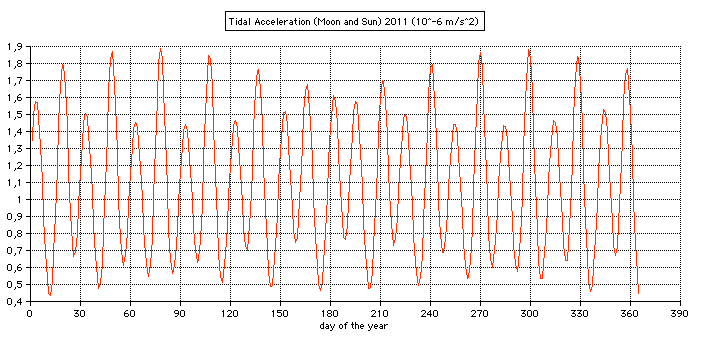 The applet is also computing the geocentric and topocentric distance of the Moon from the Earth (kilometers), the apparent angular size (arc minutes), the illuminated fraction of the Moon's disc (per cent), and the Moon's phase: 0.00 = new MoonThe altitude is taking into account the horizontal parallax of the Moon.
Select "Write Data" from the "Details" menu: 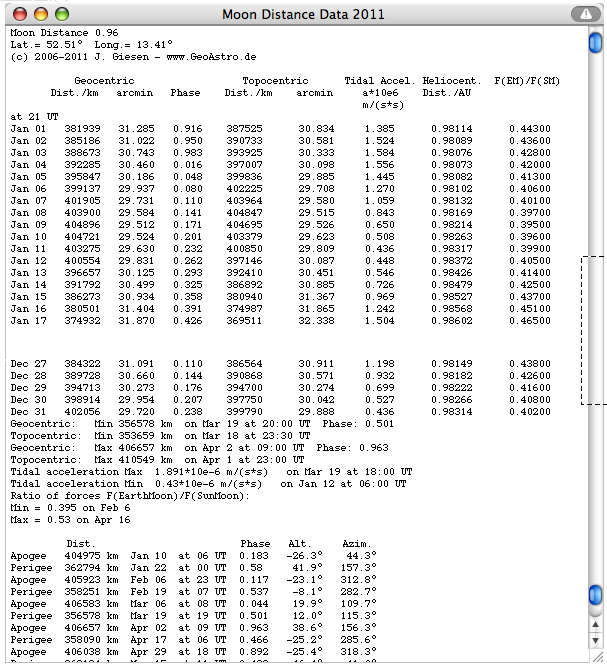 F(EM)/F(SM) is the ratio of the gravitation forces between Earth and Moon F(EM) to Sun and Moon F(SM). The mean value of about 0.45 for the Earth's Moon is unique in the solar system: Details Select "Diagram" from the Details menu: 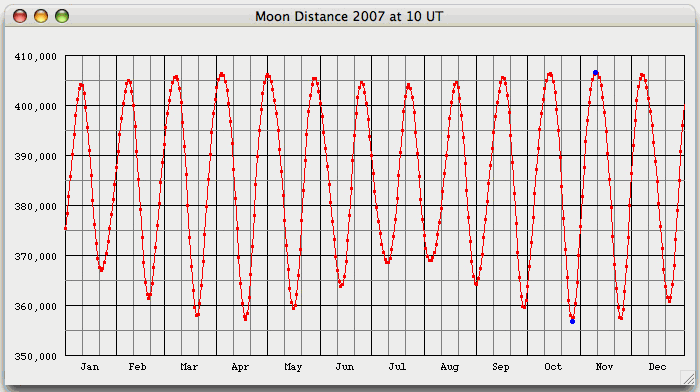 The change of distance may be up to about 6,300 km per day. The mean perigee distance of 284 anomalistic months is 362562.4 km.
|
|
|
|
Please visit my Moon Applet Collection
Visit my page: The Moon: orbit and phases
|
|
|
Gezeiten Vorhersage
(Gezeitenkalender) Gezeiten deutsche Nordseeküste (BSH)
|
| Books |
| George Howard
Darwin: Ebbe und Flut sowie verwandte Erscheinungen im
Sonnensystem, Teubner, Leipzig und Berlin, 2. Aufl.
1911. |
©
2011-2023 J. Giesen
![]()
Last
modified: 2023, Oct 06