The Mathematics of the Rainbow
|
Each internal reflection turns the
beam by 180°-2β, two refractions (in and out) turn it by
2(α-β).
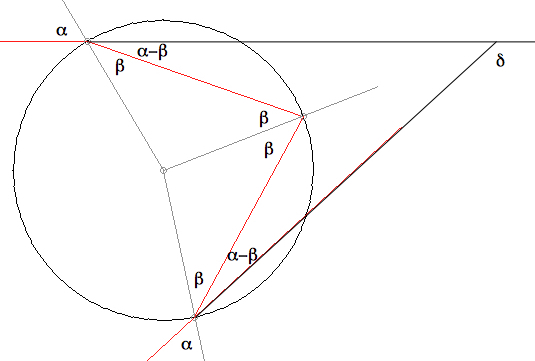 For k internal reflections the total deflexion δ is: δ = 2(α-β) + k(180°-2β) =
2α - 2(k+1)β + k 180° (1)
To find the angle α of
incidence at extremal deflexion we
differentiate the equation (1) for α and
solve for zero:
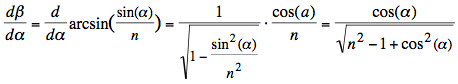 (3)
(3)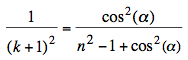 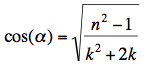 or
or 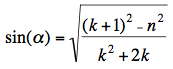 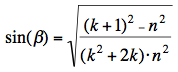 Inserting into
equation (1) for extremal deflexion:
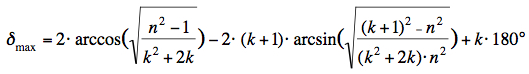 For one reflexion (primary rainbow): 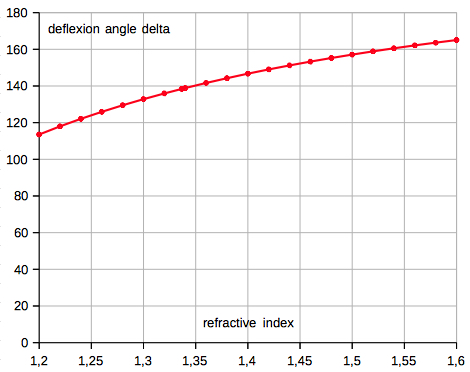 |
|
|
| The
Work of G.G. Stokes in Evaluating the Airy Rainbow
Integral and its Ramifications Today (Anne B. O’Donnell) From Alexander of Aphrodisias to Young and Airy (J.D. Jackson) The Mathematics of Rainbows (American Mathematical Society) Zwei Bemerkungen zu Airy's Theorie des Regensbogens (W. Wirtinger) |
| Books |
| Dietze, Gerhard: Einführung in die Optik
der Atmosphäre; Akadem. Verl.-Ges. Geest & Portig,
Leipzig 1957. Pernter, J. M., Exner, F. M.: Meteorologische Optik; Salzwasser Verlag, Paderborn, 2012; 978-3-86444-515-6 Nachdruck der 2. Auflage 1922 Pernter, J. M., Exner, F. M.: Meteorologische Optik; Wilhelm Braumüller, Wien und Leipzig, 2. Aufl. 1922 Vollmer, Michael: Lichtspiele in der Luft, Atmosphärische Optik für Einsteiger; Spektrum Akademischer Verlag, 978-3-8274-3092-2 (Softcover). |
2016 J. Giesen
updated: 2016, Apr 28