|
Home Astronomy How to compute the position of the
Sun Sun, Moon
& Earth Applet
 Daylight Applet Daylight Applet
How to compute the length
of a day
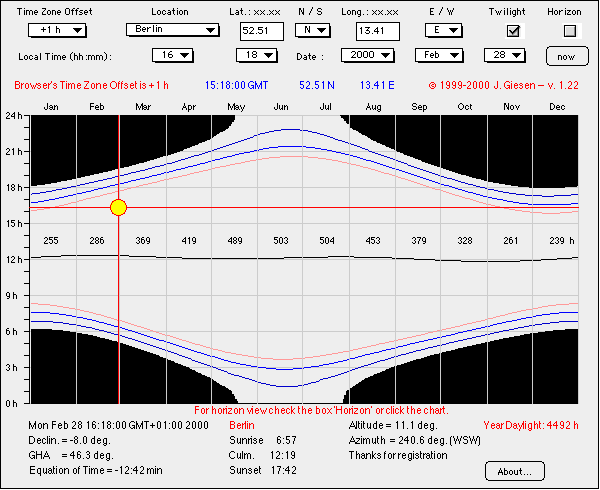
The following calculation gives an approximate value for the
length of a day from sunrise to sunset (duration of daylight) for any
location.
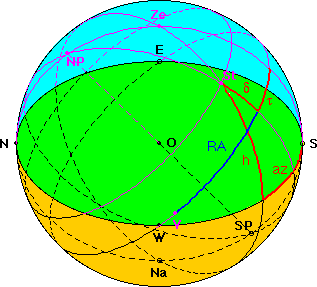
A screen shot of Walter Fendts applet
shows the "nautical triangle" of the celestial sphere for an observer
located at O: North Pole NP, Zenith Ze and
star or sun St.
The angles in this triangle are: NP-Ze = 90° - beta, NP-St =
90° - delta, Ze-St = 90° - h
|
h
|
altitude (elevation) of the
sun
|
|
beta
|
geogr. latitude of the
observer
N: beta > 0°, S: beta < 0°
|
|
delta
|
declination of the sun
measured in degrees north and south of the celestial equator
N: 0° < delta < 23.5°, S: 0° > delta > -
23.5°
|
|
tau
|
local hour angle of the
sun (Greenwich hour angle +/- longitude),
measured along the equator from the meridian
S-NP-N of the observer to the hour circle
SP-St-NP of the star St.
|
From spherical trigonometry we get:
sin (h) = sin (beta) * sin (delta) + cos (beta) *
cos (delta) * cos (tau)
At sunrise / sunset, with sin (h)=0 and dividing by cos
(beta)*cos (delta) we get:
cos (tau) = - tan (beta)*tan (delta)
For |- tan(beta)*tan(delta)| > 1 there is no sunrise or
sunset (length of day 0 hours or 24 hours ).
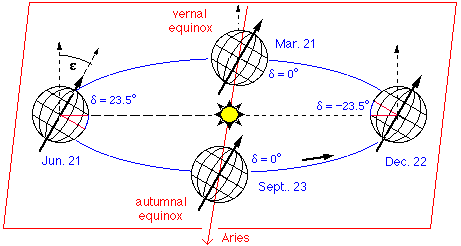
We can approximate the declination of the sun by:
delta = 23.5° * sin [(x/365)*360°]
with x = number of days since vernal equinox (about March 21)
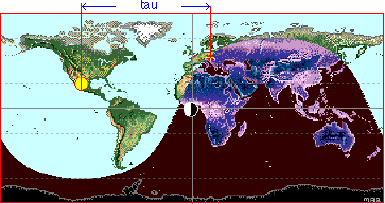
June 21, local hour angle tau for sunset
in Vienna at 20:58 local time.
Example 1:
June 21, delta=23.5°, beta=48° (Vienna), we get tau =
118.9°
corresponding to 7.93 hours (since tau=360° corresponds to 24 hours)
The Sun rises 7.93 hours before transit (culmination) and sets 7.93
hours after,
length of solar day is 15,85 hours,
exact value (from "Sun, Moon & earth Applet") is: 16.07 hours.
Example 2:
December 21, delta=-23.5°, beta=48° (Vienna), we get
tau = 61.1°
corresponding to 4.07 hours (since tau=360° corresponds to 24 hours)
Sun rises 4.07 hours before transit (Culmination) and sets 4.07 hours
after,
length of solar day is 8.15 hours,
exact value is: 8.36 hours.
More precise calculation by
my JavaScript


Last
Modified: 2008, Jan 02
|



