|
Astronomy Sun, Moon & Earth Applet
Ein vereinfachtes Verfahren zur Berechnung der Sonnenhöhe mit Tabellenkalkulation finden Sie hier
Basics of Positional Astronomy The observer is located at the centre of his "celestial sphere" with zenith Z above his head and the horizon N-E-S-W. The Sun, Moon or any other celestial body can be identified by the two coordinates altitude h and azimuth alpha (horizontal coordinates). Altitude is the angular distance above the horizon (0 < h < 90°), and azimuth the angular distance, measured along the horizon, westwards from the south point S (in astronomy) or eastwards from the north point N in nautics (0 < alpha <360°). The daily movement of an object - resulting from the rotation of the Earth on its axis - starts when it rises at (1). At (2) it passes across the observer's meridian NZS, reaching its maximum altitude above horizon (transit, culmination), and it sets at (3). Please watch the Java applet Apparent Movement of a Star (on this server, with kind permission of Walter Fendt). The horizontal coordinates of an object depend on the location of the observer on the Earth (and on time). In astronomy equatorial coordinates are commonly used when giving the position of an object on the celestial sphere. The equatorial system is based on the celestial equator, which is the great circle obtained by projecting the Earth's equator on to the celestial sphere, the equatorial plane being perpendicular to the Earth's axis of rotation.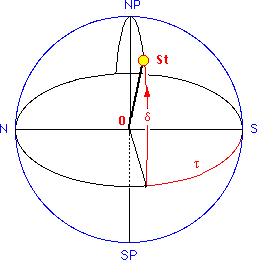 
The
first
equatorial
coordinate is declination delta,
measured in degrees north and south of the celestial equator (N: 0°
< delta < 90°, S: 0° > delta > - 90°. The
second coordinate, may be the hour angle tau, measured
along the equator from the meridian S-NP-N of the
observer to the hour circle SP-St-NP of
the star St. The hour angle corresponds to the length of sidereal time
elapsed since the body St last made a transit of the meridian.
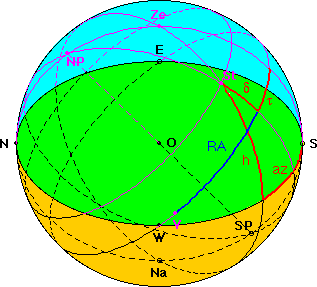 To convert equatorial coordinates hour angle (tau) and declination (delta) to horizontal coordinates azimuth (az) and altitude (h), the "nautical triangle" NP-Ze-St is used: NP-St = 90° - delta, Ze-St = 90° - h. From spherical trigonometry we get: tan az = (- sin tau) / (cos beta tan delta - sin beta cos tau) Example: Applet: Azimuth, Latitude, Hour Angle, Declination The
second
equatorial
coordinate may also be right ascension RA, measured
in hours, minutes and seconds of time, taking into account the rotation
of the celestial sphere once in 24 hours of sidereal time. The zero
point for right ascension is taken as the northern vernal
equinox.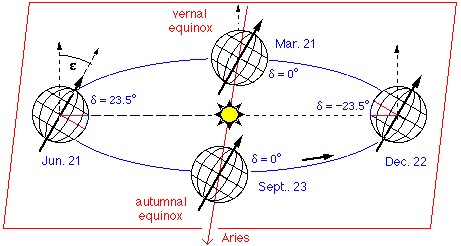 
Right ascension RA, hour angle tau and sidereal time theta are related by: tau = theta - RA Animation: |
2.
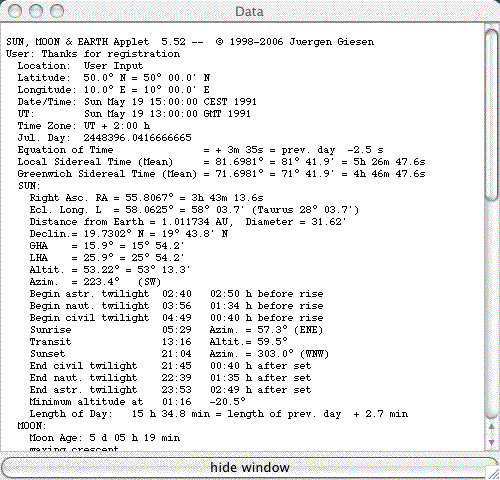
Conversion
of
date and time: local
time
to
universal time UT 15
h
CEST
= 13 h UT convert
time: Julian Day of 1991/ 5/19
at 13 UT Julian
day
of
2000/01/01
at
12 UT number
of
Julian
days since 2000/01/01 at 12 UT number
of
Julian
centuries since 2000/01/01 at 12 UT
JD
=
2448396.04167 JD = 2451545.0 -3148.95833 2. Astronomical
algorithms: compute
ecliptic longitude of the Sun
apparent
longitude latitude
B
is
assumed to be zero L
= 58.06° convert ecliptic
longitude to right ascension RA and declination delta RA
=
55.81° compute sidereal time (degree) at
Greenwich local
sidereal
time
at longitude 10° E local
hour
angle theta0
=
71.698° theta
=
theta0
+ 10° = 81.698° tau
=
theta
- RA = 81.698° - 55.81° = 25.89° 3. Final
results: convert (tau, delta)
to horizon coordinates (h, az) of the observer (50° N, 10° E)
The
function
atan2(numerator,denominator)
should be used to avoid ambiguity. altitude
angle:
h
= 53.4 °
azimuth
angle:
az
= 223.6° from N
compute the
position of the Sun on 1991/05/19 at 15:00 CEST
Berechnung des Sonnenstandes
used by the algorithm for L
T
= - 3148.95833/36525
= 0.086213780
delta = 19.73
azimuth angle: az = 223.6° - 180° = 43.6° from S
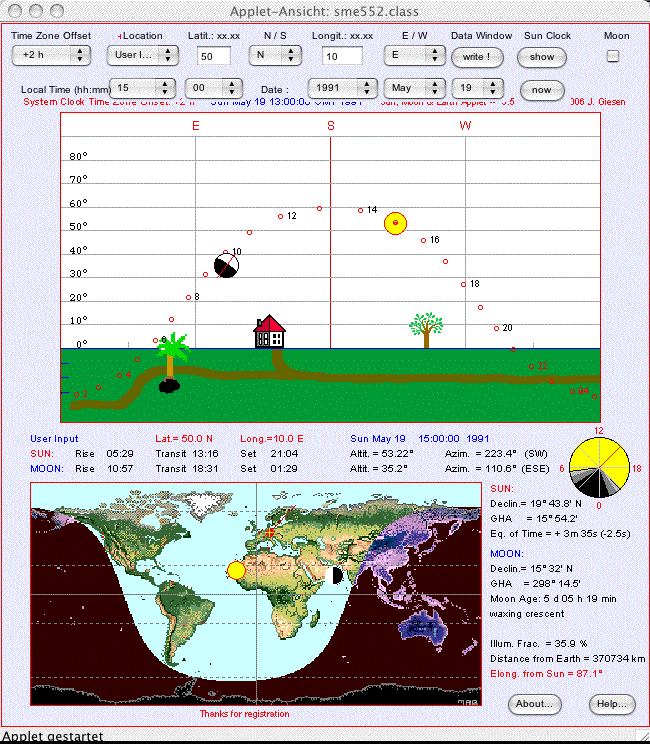
Please compare with results by my Sun, Moon & Earth Applet:
